بقلم Hassan Ghosoun

جدول المحتويات
الجبر البولياني || Boolean algebra.
علاقة الحاسوب بالجبر البولياني.
من الجداول الحقيقة إلى الدوائر الإلكترونية
الرياضيات المستخدمة في علوم الحاسوب
علاقة الحاسب الالي بجميع العلوم الاخرى.
المنطق البوليني وأنظمة الترميز.
المقدمة
لنبدأ كلامنا عن المنطق الرقمي بهذه الحقيقة العلمية: الصناعة التقنية الحالية، والأجهزة الحاسوبية التي نستخدمها اليوم – على مختلف أنواعها – وكافة التقنيات المعقدة التي يستخدمها العلماء في أبحاثهم ودراساتهم، تعتمد جميعها على مبدأ بسيط واحد، وهو تمثيل المعلومات باستخدام عددين، هما الصفر (0) والواحد (1). هذين العددين، هما الأساس في كل ما يتعلق بالحواسيب، والدارات المتكاملة، وكل أشكال المعلومات، من صورٍ لفيديوهات لنصوص لبرامج وتطبيقات وغيرها، ليست سوى أشكال متنوعة لسلاسل طويلة من الأصفار والواحدات.
الكلام السابق يتطلب التوضيح، وهو ما نود القيام به عبر هذا المقال، الذي سنخصصه للحديث عن أسس المنطق الرقمي، وعلاقته بالإلكترونيات الرقمية، والدارات المتكاملة، والمعالجات الحاسوبية، وكافة المظاهر التقنية الحديثة التي نستخدمها بحياتنا اليومية، ربما بدون أن نعرف كيف تعمل بشكلٍ فعليّ.

المنطق || المنطق في كل مكان
أجهزة الكمبيوتر والمنطق لا ينفصلان – أليس كذلك؟ هم الآن ولكن في البداية كانت الأمور أكثر ضبابية.
تم تصميم أجهزة الكمبيوتر الأولى كمحركات حسابية تلقائية ، بينما كان منشئوها يدركون أن المنطق له علاقة بكل شيء، إلا أنه لم يكن واضحًا بنسبة 100٪ فيما يتعلق بالكيفية أو السبب.
حتى اليوم ، نحن نميل إلى المبالغة في تبسيط المنطق ودوره في حساب وفهم العالم ، وكان جورج بول الرجل الذي بدأ كل شيء على القمة مع عناوين كتبه حول هذا الموضوع – التحليل الرياضي للفكر والتحقيق في قوانين الفكر .
وضع عمل بول المنطق الحديث على الطريق الصحيح بالتأكيد، لكنه أيضاً بالتأكيد لم يكن له أي علاقة بـ “قوانين الفكر .”حقيقة الأمر هي أنه حتى اليوم ليس لدينا فكرة واضحة عن القوانين التي تحكم الفكر وإذا فعلنا موضوع الذكاء الاصطناعي بأكمله فسيكون موضوعًا مغلقًا.
ما فعله جورج بول ليتم الاعتراف به كأب لتكنولوجيا المعلومات الحديثة هو التوصل إلى فكرة كانت في الوقت نفسه ثورية وبسيطة.
يشير هذا الفيديو ، وهو مقطع دعائي لفيلم وثائقي يحتفل بالذكرى المئوية الثانية لميلاده في الثاني من نوفمبر عام 1815 ، إلى كيف يدعم اكتشافه الجذري العصر الرقمي:
الجبر البولياني || Boolean algebra
قبل الحديث عن العناصر الإلكترونية الرقمية وكيفية عملها، وكيفية قيامها بمعالجة المعلومات والبيانات، علينا أن نسلط الضوء على أحد الفروع الهامة في الرياضيات، وهي “الجبر البولياني Boolean Algebra”.
تاريخياً، فإن الجبر البولياني قد تم ابتكاره عبر عالم الرياضيات البريطاني

“جورج بول|| George Frederik Boole”
(November 2, 1815 – December 8, 1864)،
الذي كان معاصرلتشارلز باباج، حيث التقى به لفترة وجيزة ، وبول هو في هذه الأيام يعتبر “جد عصر المعلومات”. في عام 1849 أصبح أول أستاذ للرياضيات في كلية كوينز الجديدة في أيرلندا (أصبحت الآن كلية جامعية) كورك. توفي عن عمر يناهز 49 عامًا عام 1864 ، وربما لم يكن لأعماله تأثير على علوم الكمبيوتر دون كلود شانون ، الذي أدرك بعد 70 عامًا أهمية هندسة المنطق الرمزي لبول. ونتيجة لذلك ، أصبح تفكير بول الأساس العملي لتصميم الدوائر الرقمية والأسس النظرية للعصر الرقمي.
يعود لبول الفضل في وضع الأسس الرياضية للمنطق المستخدم في توصيف أنظمة العد الثنائية وعمل البوابات المنطقية الأساسية، وبالتالي أساس المنطق الحاسوبي الحديث حيث استخدم رموز الجبر للدلالة على العلاقات المنطقية فكان له الفضل في الفهم الحديث للعلاقات بين الموضوعات على أسس القوانين الجبرية. بمعنى، أن الشيء إما أن يكون موجودا أو غير موجود، أو أن الشيء إما أنه حاضر أو غائب، أو أن الشيء دائر أو عاطل، الخ.
وقد قدمه للمرة الأولى في كتابه “التحليل الرياضي للمنطق The Mathematical Analysis of Logic ” والذي صدر عام 1847. وفي عام 1854، قام جورج بول بتقديم أسس الجبر البولياني بشكلٍ واسع في كتابه الأشهر “دراسة في قوانين التفكير An Investigation of the Laws of Thought[1] ”.
ومن الاسم، فإن الجبر البولياني هو أحد فروع علم الجبر في الرياضيات، ولكنه بخلاف الجبر الاعتيادي، فإنه يفترض تواجد المتحولات الرياضية ضمن ما يعرف بـ “ قيم الحقيقة Truth Values ” وهي: القيمة الحقيقية True، القيمة الخاطئة False. بالتالي، فإن كل الأرقام والأعداد التي يتم التعامل معها في الجبر العادي، تتحول في الجبر البولياني لتركيباتٍ من الحالات الحقيقية Truth والخاطئة False . لسهولة التعامل، تم إسناد قيمة “1” للحالة الصحيحة، وقيمة “0” للحالة الخاطئة . وبالتالي، فإن أساس الجبر البولياني هو التعامل مع كافة المعطيات استناداً لقيمتين مرجعيتين: 0 و 1.
الاختلاف الآخر الذي يميز الجبر البولياني عن الجبر العادي هو العمليات الرياضية، ففي حين أن الجبر العادي يعتبر أن العمليات الأساسية فيه هي الجمع والطرح والضرب والقسمة، تعتبر العمليات الأساسية في الجبر البولياني هي: عملية الاقتران Conjunction ، وعملية الفصل-اللااقتران Disjunction ، وعملية النفي Negation .
إذاً، فإن أساس الجبر البولياني هو قيمتين تدعيان بقيم الحقيقة، وثلاثة عمليات رياضية أخرى ، حيث يهيء إجراءا رياضيا لتداول العلاقات المنطقية في شكل رمزي. فالمتغيرات البوليانية تخضع لحالتين أو قيمتين لا غير، فالقيم الزوجية المحتملة هي (نعم ،لا) أو (فَتْح ،قَفْل) أو (صواب، خطأ). ومن الشائع في مجال الأعمال الهندسية استخدام الواحد والصفر (1, 0) كرموز للمتغيرات البوليانية. وتستخدم الكمبيوترات إشارات لها حالتان أو قيمتان احتماليتان. فالجبر البولياني يجعل في إمكان مصممي الكمبيوترات تجميع تلك المتغيرات رياضيا وتداولها بطريقة تسمح بتكوين أبسط التصميمات التي تهيء الوظيفة المنطقية المطلوبة. ففي الجبر البولياني، يمكن التعبير عن بعض الافتراضات مثل:
C = A AND B
التي تعني أن C تكون صحيحة إذا كانت A صحيحة، كما يتحتم كذلك أن تكون B هي الأخرى صحيحة. كما يستخدم أيضا الجبر البولياني في البوابات في دوائر الكمبيوتر الإلكترونية. فكما أن الصفر والواحد يعبران عن القيم المنطقية، فيمكن استخدام مقارنة الحالات الفيزيائية للدائرة، كما في الفولط، وكما في البوابات المنطقية logical gates، فهي تتحكم في سريان التيار الكهربائي (بتات البيانات) وذلك لتمثيل AND, OR, NOT والمعاملات البوليانية الأخرى.
وفي الكمبيوتر تنضم تلك البوابات المنطقية حيث تكون مخرجات إحدى البوابات هي مدخلات بوابة أخرى، بحيث تكون النتيجة (وهي تتألف من الآحاد والأصفار) ذات مغزى.
[1] An investigation of the laws of thought, on which are founded the mathematical theories of logic and probabilities.” “بحث في قواعد التفكير كأساس للنظريات الرياضية عن المنطق والاحتمالات”
علاقة الحاسوب بالجبر البولياني
الحاسوب Computer هو مثل باقي الآلات التي اخترعها دماغ الإنسان لكي تساعده في أداء مهامه وإنجاز أعماله، كما اخترع السيارة لتقريب المسافات.
هذه الآلة قطعت أشواطا كبيرة منذ أن تم اختراع أول حاسوب سنة 1948 حيث كان في البداية كبير الحجم و معقد الاستعمال ، يتطلب كفاءة علمية دقيقة، إلى إن أصبح في متناول الأشخاص العاديين دون الحاجة إلى التخصص في الرياضيات أو الإلكترونيات .
تعريف الحاسوب:
يرتكز الحاسوب على أساسين: الأساس الرياضي الذي يعتمد على الحساب أو النظام الثنائي (code binary ) يتكون من رمزين : الصفر(0) أو الواحد (1) و هو بمثابة لغة الحاسوب التي يتواصل بها و هو الذي يسمح بمعالجة الحروف الهجائية و الأرقام… أما الأساس الإلكتروني فيشتمل على “الترانزيستور || transistor” ، عبارة عن دارة إلكترونية تتخذ حالتين مستقرتين وهما وجود التيار الكهربائي (1) أو غيابه (0).
اشتغال الحاسوب :
إن الحاسوب هو مجرد آلة لتنفيذ الأوامر المتتابعة التي يتلقاها من برنامج معلوماتي computer program.مستعملا ” الحساب الثنائي” و” الجبر البولي” كمبدأ اشتغال و الإلكترونيات كتقنية .
علوم الحاسب الالي[2] كما ذكرت علوم مستحدثة ظهرت مؤخرا من زمن ليس ببعيد واكثر العلوم تطورا والحاسب الالي أيضاً مبني علي مجموعة من العلوم السابقة كما نشاهد ولكن الان جميع العلوم في مختلف المجالات تستعمل الحاسب الالي وهو يبين لنا مدي التطور الهائل لهذا العلم ومدي تطور التكنولوجيا …
تطبيقات الحاسب الالي موجودة في جميع العلوم
طبعا كلنا نعلم دخول الحاسب الالي كل المجالات والعلوم والابحاث وسوف اذكر على سبيل الذكر:
علاقة الحاسب الالي وعلم الرياضيات:[3]
طبعا كلمة حاسب مأخوذة من الحسابات او الارقام وعلم الرياضيات فنلاحظ في الحاسب الالي يوجد المنطق الرياضي والاستنتاج والمصفوفات والمتسلسلات والمحددات وهذا هو علم الجبر فرع من علم الرياضيات، ونلاحظ ايضا تطبيقات الاحتمالات في البرامج وايضا مبادئ التحليل العددي وحلول التفاضل والتكامل والمعادلات التفاضلية كل هذا نستخدمه في البرامج في الحاسب الالي ونلاحظ ايضا نظرية الخوارزميات وكيفية تحليل المشكلة البرمجيه وكثير وكثير…. فالبرمجة كما ستلاحظون بها اشياء كثيرة رياضيه ولكن سهلة جدا ليس كما تتصورون…
[2]علوم الحاسوب (اركز هنا على كلمة علوم) وليس هندسة البرامج او البرمجة( ربما تشرحها كلمة واحد من اشهر العلماء في علوم الحاسوب حول الخلط بين هذه المفاهيم:
“computer science is no more about computers than astronomy is about telescopes
[3] وللمزيد انظر ملحق علاقة الحاسب الآلي بجموع العلوم الآخرى
من الجداول الحقيقة[4] إلى الدوائر الإلكترونية
لا يوضح هذا العرض التوضيحي الصغير فقط لماذا يكون منطق Boolean مفيدًا في تصميم مثل هذه الأنظمة ، ولكنه يفسر أيضًا سبب كون دوائر الإلكترونيات لأداء منطق Boolean شائعة. يمكنك شراء دوائر متكاملة تؤدي And و Or و Not والعديد من المجموعات الأخرى من هذه العمليات في حزمة واحدة سهلة الاستخدام.
أين هي “الحقيقة” في هذا؟
من الواضح أن المنطق البولياني يعمل مع “صواب” و “خطأ” وهذا هو بالضبط ما فكر به بول نفسه ، ومع ذلك يمكنك العمل مع نفس نظام العاملين والنتائج بغض النظر عن ما تسميه الحالتان – لأعلى / لأسفل ، on/off أو صفر / واحد.
في حالة الإلكترونيات ، من الطبيعي أن تفكر في الجهد العالي والمنخفض على أنه يمثل الحالات الطبيعية التي نعمل معها .غالبًا ما يكون التفسير الذي يتضمن المنطق البولياني أكثر ملاءمة عندما يتم التعبير عنه بمصطلحات تنتمي إلى الموضوع الأساسي ، ولكنه لا يزال هو نفس المنطق البولياني.
ما علاقة كل هذا بالكمبيوتر؟
الجواب ذو شقين. الصلة الأولى هو أن أجهزة الكمبيوتر تحتوي على دوائر إلكترونية تتصرف بنفس طريقة إنذار السارق .بشكل عام ، يساعد منطق Boolean عندما تحتاج إلى تصميم دائرة يجب أن تعطي ناتجًا فقط عند وجود مجموعات معينة من المدخلات.
تسمى هذه الدائرة “المنطق التوافقي” ويوجد الكثير منها داخل الكمبيوتر. يمكنك تحديد سلوك أي جزء من المنطق التوافقي باستخدام جدول الحقيقة. الفرق الوحيد هو أنه في معظم الحالات تكون الجداول كبيرة جدًا ويعد تحويلها إلى أجهزة فعالة مهمة صعبة للغاية.
[4] انظر ملحق المنطق البولياني
المنطق في الأجهزة
ما يجعل منطق Boolean أساسيًا جدًا لأجهزة الكمبيوتر ومجموعة واسعة من الأجهزة الإلكترونية هو أن هذا المنطق سهل التنفيذ. المنطق “gate” عبارة عن قطعة إلكترونيات تأخذ بعض المدخلات وتنتج ناتجًا وفقًا لأحد الجداول المنطقية. عادة ما تكون المدخلات مرتفعة أو منخفضة ويتم تفسير ذلك على أنه 1 و 0 أو صحيح وخطأ.
على سبيل المثال ، تحتوي البوابة Not على مدخل واحد ويكون ناتجها مرتفعًا عندما تكون المدخلات منخفضة والعكس صحيح. يمكنك إنشاء دوائر منطق أكثر تعقيدًا عن طريق توصيل البوابات.
الرموز الأساسية للبوابات المنطقية الثلاثة الأساسية Not, And بالإضافة إلى exclusive Or هي:
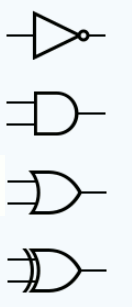
لاحظ أن الرموز القياسية الأوروبية مختلفة ولكن بشكل رئيسي لم يتم التعرف عليها.
بشكل عام ، تشير دائرة صغيرة متصلة إلى نفي أو لا – راجع بوابة ” Not .”
على سبيل المثال ، رموز NAND و NOR و Not EOR أو XNOR هي:
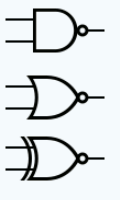
في نواح كثيرة هذه الالكترونيات تركب بشكل سهل. لا تحتاج إلى معرفة أي شيء عن الترانزستورات أو المكونات الأخرى لبناء دائرة المنطق. كل ما عليك هو معرفة التعبير المنطقي والبوابات السلكية لتنفيذه.
على سبيل المثال ، مثال الإنذار ضد السرقة لديه التعبير المنطقي:
R = Not(P) And Q
لتنفيذ ذلك في الأجهزة ، نحتاج إلى بوابة Not وبوابة: AND
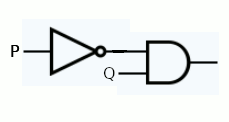
دوائر المنطق الحقيقي أكثر تعقيدًا بكثير من هذا ويمكن أن تستخدم مئات أو حتى الآلاف من البوابات.
الحساب الثنائي
الصلة الثانية هي في الواقع مجرد حالة خاصة من الأولى لكنها مهمة للغاية، وغالبا ما يربك الناس أنه يمكن استخدام المنطق البولياني لتنفيذ الحساب الثنائي.
لاحظ أنه لا يوجد ما يشير إلى أن المنطق الثنائي والحساب المنطقي هما نفس الشيء – ليسوا كذلك. الحساب الثنائي هو مجرد مثال لنظام القيمة الموضعية لتمثيل القيم. بمعنى ، نحن البشر يعملون بقاعدة العشر أصابع وتجد أجهزة الكمبيوتر أنه من الأسهل العمل في القاعدة الثانية لأنهم لا يمتلكون عشرة أصابع.
ومع ذلك ، عند قيامك بحساب ثنائي ، تتبع القواعد القياسية التي تحدد كيفية دمج البتات معًا لإنتاج البتات الناتجة. يمكن التعبير عن هذه القاعدة كمنطق اندماجي – بمعنى آخر ، جدول الحقيقة.
يمكنك بسهولة إنشاء جدول يوضح كيفية إضافة وحدتين معًا لإعطاء نتيجة وحمل إلى المكان التالي:
A B Result Carry
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
اذا كنت لا تعرف كيفية إضافة وحدتين معًا ، فقم ببساطة بقبول الجدول كإرشادات لكيفية القيام بذلك.
يمكنك أن ترى أن هذا مجرد جدول حقيقة آخر ، ويمكن إنتاج المنطق التوافقي اللازم لذلك بالطريقة المعتادة. في الواقع ، هذا ليس سوى نصف الجامع – نعم هذا هو المصطلح الفني الحقيقي – لأنه لا يضيف قيمة حمل قد يكون تم إنشاؤها بواسطة زوج من وحدات البت السابقة.
جدول “الجامع الكامل” ، هذا هو أيضًا المصطلح التقني الصحيح:
A B C Result Carry
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
تعد الدارات التوافقية هي الرابط الرئيسي بين منطق Boolean وأجهزة الكمبيوتر ، ولكن يوجد ما هو أكثر من أجهزة الكمبيوتر من المنطق التوافقي.
في بعض الأحيان سوف تسمع أجهزة الكمبيوتر المشار إليها قطعة واحدة فقط من منطق بوليان ولكن هذه هي المبالغة. قطع كبيرة هي مجرد بوابات And ، Or ، Not ولكن هناك أيضًا قطع ضخمة لا يمكن وصفها من حيث المنطق البولياني البحت.
القلاب[5]
تتضمن أجهزة الكمبيوتر أيضًا المنطق “المتسلسل” ، والذي يتضمن عنصر الوقت.
على سبيل المثال ، فإن flip-flop ، المصطلح الجيد تمامًا مرة أخرى ، عبارة عن دائرة تتغير حالة مثل رقاص الساعة يتقلب من جانب إلى آخر.
الشيء الغريب هو أنه يمكنك إنشاء قلاب من بوابتين وليس بوابات ، وصحيح أن معظم المنطق المتسلسل يمكن فهمه من حيث مجموعات البوابات المنطقية. ومع ذلك ، هذا تفسير غير كامل ويتطلب شيئًا يتجاوز المنطق البولياني.
على سبيل المثال ، لا يستطيع منطق Boolean التعامل مع العبارة:
A = NOT A
إذا كانت الإجابة “A” صحيحة ، فإن “A” ليست “خاطئة” و “A” يجب أن تكون خاطئة ، لكن هذا يعني أن “A” غير صحيح ، مما يعني أن “A” يجب أن يكون صحيحًا ، يعني ، وهكذا …
لذلك من وجهة نظر المنطق البولياني هذا هراء. ?
الآن تخيل أنك على جانب واحد من السبورة تكتب “A صحيح” وعلى الجانب الآخر تكتب “Not A is true”. الآن عندما تقرأ “A صحيح” ، فأنت سعيد بهذا. عندما تقوم بإدارة السبورة ترى “ليس A صحيحاً” وهكذا تستنتج A غير صحيحة. بينما تستمر في قلب اللوحة فوق قيمة A من تتقلب من صح إلى خطأ والعودة مرة أخرى.
هذا التحول في السبورة هو الجزء الإضافي من النظرية اللازمة للتعامل مع المنطق المتسلسل – فهو يوضح كيف يغير الوقت الأشياء. لذا فإن أجهزة الكمبيوتر ليست مجرد عبارة واحدة كبيرة في منطق Boolean ، والتي تصادف أنها صحيحة أو خاطئة.
تتغير حالتها مع كل علامة من ساعة نظامها.
بالإضافة إلى جبر Boolean أعلاه ، تم تطوير بوابات المنطق الرقمي لتمثيل تعبيرات Exclusive OR و Exclusive NOR لتوسيع النطاق الأصلي لقوانين Boolean. راجع تعبيرات OR Exclusive .
وقد تحتوي البوابات المنطقية على اثنين أو أكثر من المدخلات ، وباستثناء بعض الحالات الخاصة، يكون لها خرج واحد. لا يمكن أن تكون حالة طرفي الدخل والخرج إلا في أحد الشرطين الثنائيين ، إما منخفض (0) أو مرتفع (1) ، ويمثله مستويان مختلفان للجهد ، عادةً 0 فولت للمنطق 0 وحوالي 3 إلى 5 فولت للمنطق 1 ، اعتمادا على تكنولوجيا أشباه الموصلات المستخدمة. البوابات المنطقية تتطلب أيضًا مصدر طاقة.
[5] ( Introduction to Boolean Logic , n.d.)
الترانزستور كمحول[6]
تصنع البوابات الإلكترونية عمومًا من دارات الترانزستور التي تعتمد على تشغيلها على استخدام الترانزستور كمفتاح ، بدلاً من كونها مضخم صوت تم اختراعه في الأصل .مع عدم وجود جهد على القاعدة ، لا يوجد تيار من خلال الترانزستور الذي يتم إيقاف تشغيله وبالتالي سيكون جهد الخرج (جامع) عاليًا. عندما يتم تطبيق الجهد “العالي” على القاعدة ، يتم تشغيل الترانزستور ويكون جهد الخرج (جامع) “منخفضًا”. انظر المزيد على الصفحة حول أشباه الموصلات .
كانت النسخة المبكرة من دائرة التبديل ثنائية الاستقرار هي 1919 Eccles and Jordan flip-flop استنادًا إلى الصمامات (الأنابيب المفرغة). كانت نسخة الترانزستور اللاحقة واحدة من أولى الدوائر الإلكترونية التي طبقتها روبرت نويس كحلقة متكاملة في عام 1959.
تعتمد عمليات التقليب على مفهوم التغذية المرتدة التي يتم فيها إعادة إخراج الدائرة مرة أخرى إلى المدخلات ، بحيث يكون الناتج منخفضًا والعكس صحيح عندما يكون الدخل مرتفعًا.
انظر الارتباط التشعبي على مثال مفاتيح الترانزستور المستخدمة في الدائرة الإلكترونية المستخدمة لتنفيذ بوابة NOR ثلاثية الدخل .
[6] (Boolean Logic and Digital Circuits, n.d.)
دارة الجامع الثنائية البسيطة[7]
ومثال آخر دارة الجامع الثنائية البسيطة التي تظهر كيف يمكنك إضافة أرقام ثنائية مع البوابات. إذا كان يمكنك إضافة ، فهذا يعني أنه يمكنك طرح أيضا. إذا استطعت طرحها ، يمكنك إجراء مقارنة أيضًا (مما يعني أنه يمكنك القيام بذلك إذا / ثم ، حلقات ، وما إلى ذلك.) لذلك يصبح هذا جزءًا رئيسيًا من أي برنامج تقريبًا.
يمكنك أيضًا الانتقال من هناك إلى الأجهزة الحكومية لإظهار كيف يمكنك إنشاء آلات في العالم الحقيقي مثل إشارات المرور والمصاعد وما إلى ذلك ، عبر أجهزة Moore / Mealy state باستخدام البوابات المنطقية بدلاً من البرامج التقليدية. في هذه الحالة ، يعمل) Flip / Flops الذي تم إنشاؤه أيضًا من بوابات المنطق الأساسية) كذاكرة 1 بت لتذكر “الحالة” الحالية كرقم ثنائي. ثم على نبض الساعة ، تجمع مجموعة من المنطق التوافقي بين مدخلات النظام ، مثل أزرار الضغط أو أجهزة الاستشعار الأخرى ، مع القيمة الحالية للحالة ، والتي تنتج كلا من مخرجات المنطق (مثل تشغيل الضوء الأحمر) ، وتقرر ما الحالة التالية للانتقال إلى ستكون (أو ربما تبقى في نفس الحالة). ثم ينتظر النظام نبض الساعة التالي.
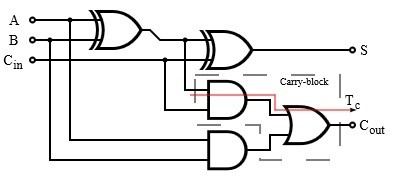
مثال على الرسم البياني للجامع ، والذي يأخذ اثنتين من البتات لإضافته إلى وحدة بت اختيارية للحمل ، وينتج مجموع ومخرجًا للحمل الخاص لبتة الجامع التالية ، باستخدام منطق XOR و AND و OR:
“الرسم التخطيطي لمنطق الجامع الكامل” بواسطة inductiveload – الرسم الخاص ، Inkscape 0.43. مرخصة بموجب المجال العام عبر العموم
مثال عن الحالة ماكينة الباب الدوار:
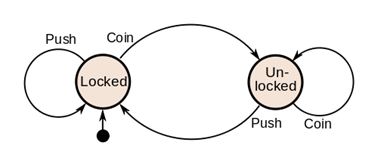
[7] (By Chetvorno (Own work) [CC0], n.d.)
المنطق البولياني في البرمجة
مثال آخر وعلى نطاق الحب والغزل … يصلح للرجل ان يقوم بحمل فتاته الجمليه واركابها على حصانه ومن ثم قضاء نزهه جميله وان يقوم بشي اللحم وتقديمه لها … والان قل لي هل يصلح العكس اي …
ان تقوم المرأه بحمل <<< الرجل وتركيبه على حصانها وشي اللحم وتقديمه اليه .
واتمنى ان تفهم ما من وراء ذلك !! ??
الا يندرج ما نتحدث عنه تحت المنطق ؟؟
بل هناك مثال ابسط من هذا لك :
ماذا لو قلت لك اصنع برنامج ياخذ اسم شخص كاملا وياخذ تاريخ ميلاده وتاريخ ميلاد والده واجداده
ألا تستطيع ان تضع في البرنامج الكود الكافي لرفض تواريخ ميلاد غير منطقيه ؟؟؟؟؟
الشروط بسيطه…
الأب اكبر من الإبن على الأقل بمرحلة البلوغ هذه هي القاعده , الا تستطيع استخدامها في برنامجك ؟؟؟؟؟؟
الا تستطيع وضع اي شروط منطقيه طالما معك قواعد هذا المنطق ؟؟؟؟؟
منطق بوليان [8] أمر أساسي لتصميم أجهزة الكمبيوتر حتى لو لم يكن القصة كلها. الشيء نفسه ينطبق على البرمجة.
يحتاج البرنامج أيضًا إلى عنصر الوقت المضمن فيه لجعله يعمل وهذا الأمر يتجاوز حدود المنطق البولياني البسيط. ومع ذلك ، هناك أوقات يخذل فيها التفكير المنطقي البسيط حتى أفضل مبرمج.
على سبيل المثال ، مهمة شائعة هي اتخاذ قرار باستخدام عبارة IF:
IF (A>0 AND A<10) نفذ شيئًا
القوس الذي يلي IF هو منطق بولياني تقريبًا ، ويتم تنفيذ الشيء فقط إذا كان هذا صحيحًا.
حتى الآن بسيط جدًا، البسيط جدًا في الواقع أن العديد من المبرمجين يقررون أنهم لا يحتاجون إلى معرفة أي شيء عن المنطق البولياني على الإطلاق ؛ وهذا خطأ خطير.
فكر في كيفية تغيير هذا المثال حتى يتم تنفيذ “شيء ما” عندما يكون الشرط خاطئًا. أبسط طريقة هي الكتابة:
IF NOT(A>0 AND A<10) نفذ شيء
لكن هذا يسيء إلى بعض المبرمجين الذين يرغبون في إعادة كتابة الشرط الذي لا يستخدم NOT.
جربه وانظر ما توصلت إليه.
الخطأ الشائع هو استخدام:
IF (A<=0 AND A>=10) نفذ شيء
هذا غير صحيح ، وإذا كنت لا تصدق ذلك ، فاكتب ببساطة جدول الحقيقة لكليهما. الصحيح نفي الشرط بـ Not :
IF (A<=0 OR A>10) فعل شيء
يعمل التبديل من AND إلى OR على صدم العديد من المبرمجين ذوي الخبرة وهو مصدر لأخطاء البرمجة العديدة.
نصيحتي هي أنه إذا كان بإمكانك كتابة شرط منطقي في شكل طبيعي ولكنك تحتاج حقًا إلى “NOT” ، ثم اكتب ” NOT ” أمامه!
خلاف ذلك تعلم قوانين دي مورغان:
NOT (A AND B) = NOT(A) OR NOT(B)
و
NOT (A OR B) = NOT(A) AND NOT(B)
المنطق البولياني مهم كوسيلة أساسية للتفكير في المواقف البسيطة للغاية التي تتضمن مجموعات من حالتين.
ما ليس هو نظرية الفكر أو طريقة عمل أجهزة الكمبيوتر. ليس من الضروري حتى تصميم أو استخدام الكمبيوتر ، لكنه يجعل كلا المهمتين أسهل.
إذا كنت جاداً بشأن الحوسبة ، فأنت بحاجة إلى أن تحكم استخدام المنطق البولياني بنفس الطريقة التي تحكم بها الحساب – الحساب الثنائي بالطبع.
إذاً يستخدم المنطق البولياني[9] في كل لغة برمجة تقريبًا. برمجة الكمبيوتر هي استخدام رئيسي للمنطق البولياني. لأنها تتيح لنا ترجمة مشاكل العالم الحقيقي إلى رمز الكمبيوتر.
C و C ++ و C # هي ثلاث لغات برمجة كمبيوتر مختلفة تستخدم بناء جملة متشابه للغاية. يمكننا أن ننظر في كيفية استخدام منطق Boolean في هذه اللغات ، مع ذلك ، يتم تمثيل العوامل and, or, and not بواسطة رموز مختلفة لتلك المستخدمة في الرياضيات.
العوامل
العوامل المنطقية
logical and & (also bitwise), && (short-circuit) logical or | (also bitwise), || (short-circuit) logical negation !
عوامل المقارنة
العوامل التي تسير على ما يرام مع العوامل المنطقية هي:
يساوي == أقل من < اقل او يساوي <= أكثر من > أكبر من أو يساوي >= لا يساوي !=
العوامل الآخرى
الثلاثي الشرطي ? :
عبارة إذا
يتم استخدام عوامل التشغيل المنطقية هذه لإنشاء عبارات منطقية من خلال بدء العبارة بـ if .
لاختبار القيم التي يتم تخزينها في متغيرين يدعيان A و B ثم:
If (A > 5 && B < 20)
إذا كان البيان صحيحًا ، فسيستمر رمز البرنامج في العبارة التالية. إذا كانت العبارة المنطقية خاطئة ، فإن الرمز يتخطى العبارة التالية.
تتم قراءة هذا البيان كـ: إذا كانت A أكبر من 5 و B أقل من 20 ، فقم بمعالجة السطر التالي.
في الواقع الفعلي ، إذا كانت البيانات يمكن أن تتعامل فقط مع القيم المنطقية ؛ إما صحيحة أو خاطئة
حيث s عبارة عن سلسلة (أي ليس متغير منطقي)
s == “example” على الرغم من أن s و “example” عبارة عن سلاسل وليس متغيرات منطقية ، s == “example” هي معادلة لذلك تنتج قيمة منطقية ، ولهذا السبب يمكنك استخدامها في عبارة if .
حتى بعد برمجة المساواة أو علامة المساواة في هذه المسألة ، هو في حد ذاته نوع من المشغل ، فهو ليس عامل حسابي مثل الجمع أو الضرب ، بل عامل منطقي.
x و y في التكافؤ x == y يمكن أن يكون أي شيء (ضمن البرمجة ؛ مقيدًا بأنواع البيانات أو أنواع الكائنات الممكنة) ولكن نتيجة x == y) حيث يُعتقد == كمشغل) هي منطقية ؛ إما صحيحة أو خاطئة.
باستخدام الجبر المنطقي لتبسيط التعليمات البرمجية
تذكر أنه في الحساب، تستوعب العوامل الثنائية + و × ومقلوبيهما− و ÷ اثنين من المدخلات وتخرج قيمة.
في الجبر البولياني، علامة التساوي نفسها هي أيضًا عوامل تشغيل . خذ هذه المعادلة البسيطة
x=10
أيا من هذه القيم المنطقية بأي حال من الأحوال ، فإن LHS[10] و RHS[11] عبارة عن تعبيرات ، لا تكون هذه صحيحة أو خاطئة ، ولكن مع علامة المساواة ، ستنتج المعادلة (التعبير المنطقي) القيمة المنطقية ، إذا كان الإدخال x هو يساوي 10 ، ثم الناتج سيكون “صوابًا” ، إذا كانت x ليست 10 ، فسوف يخرج قيمة false. لا يمكنك إشراك الأرقام مباشرةً في الجبر المنطقي ولكن يمكنك إشراك المعادلات.
في ما يلي ، يجب أن تساوي x 10 و y يجب أن تكون 15 للتعبير عن القيمة الحقيقية.
(x=10) ∧ (y=15)
يتم كتابة التالي في [12]Pseudocode حيث “==” يمكن أن تعني مساوية = ، أي ما يعادل ⇔ or identical to ≡ أو مطابقة. في الكثير من اللغات ، يعني x = 255 من تلقاء نفسه أنك تقوم بإسناد القيمة 255 للمتغير x ، وأحيانًا ستستخدم “: =” للتخصيص لتوضيح ذلك.
حيث يكون x هو متغير منطقي و f إجراء.
If (x==true) {
f () ؛
}
If (x) {في معظم لغات البرمجة ، من الممكن إزالة "== true" لأن x بحد ذاته عبارة.
f () ؛
}
المعادلات مثل “==” هي الأكثر استخدامًا ولكن مع معرفة الجبر المنطقي ، لا يلزمك استخدامها في كل وقت. وبسبب هذا يمكنك تبسيط
If (x == true and y== true) {
f () ؛
}
مثل
If (x and y) {
f () ؛
}
لأن “x و y” نفسها تنتج قيمة منطقية.
يمكنك أيضًا استخدام ما يلي بدلاً من التكافؤ:
أكبر من:>
أقل من: <
أكبر من أو يساوي:> = أو => حسب اللغة.
أقل من أو يساوي: <= أو = <حسب اللغة.
لا يساوي:!
قد لا يكون المشغل علامة التعجب “!” أو كلمة “لا” ، ولهذا السبب ، لا تحتاج إلى الكتابة
If (x! = true) {
f () ؛
}
(! x) {يمكنك تقصير ذلك واكتب فقط إذا
f () ؛
} </code>
If (Not x) {أو
f () ؛
}
تعيين المتغيرات البوليانية
مثال برمجي مكتوب بلغة جافا: كتابة جميع القواعد التي تحكم العمليات المنطقية: جداول الحقيقة، قانون دمورغان[13].
[8] (Introduction to Boolean Logic ، بلا تاريخ)
[9] (Boolean logic in Programming Languages، بلا تاريخ)
[10] Left-hand side of something, in particular the Left-hand side and right-hand side of an equation in mathematics
[11] The opposite of LHS
[12] او مايعرف بلغة الخوارزميات
[13] (دحروج)
البوابة العالمية [14]
الحاسمة وعميقة الفكرجزئياً.
كم عدد المشغلين الذين تحتاجهم لتنفيذ منطق بولياني؟
الإجابة الواضحة هي ثلاثة – AND ، OR و NOT – ولكن هذا غير صحيح.
الإجابة الصحيحة هي أنك تحتاج فقط إلى عملية واحدة. من الواضح أنه لا يمكن أن يكون مجرد أي عملية. على سبيل المثال ، من المستحيل إنشاء OR من مجموعات AND – جربها.
ومع ذلك ، إذا قمت باختيار عملية تتضمن عنصرًا في عامل التشغيل NOT ، فيمكنك إجراء أي شيء تريد استخدامه.
على سبيل المثال ، عامل التشغيل AND ليس عالميًا ولكن NAND ، بمعنى آخر Not AND جدول الحقيقة لـ NAND هو فقط NOT(P AND Q):
P Q P NAND Q
F F T
F T T
T F T
T T F
لجعل ليس كل ما عليك فعله هو الكتابة:
P NAND P = NOT (P)
P P P NAND P
F F T
T T F
بمجرد حصولك على NOT ، يمكنك إنشاء AND:
NOT (P NAND Q)= P AND Q
العملية الوحيدة المتبقية هي جعل OR من NAND و NOT والحل لهذا هو أحد قوانين De Morgan:
NOT (P AND Q) = NOT(P) OR NOT(Q)
القليل من العمل سرعان ما يعطي:
NOT(P) NAND NOT(Q)=P OR Q
لذلك مع مشغل NAND ، يمكنك بناء NOT و AND و OR. هذا يعني أن المشغل الواحد يفعل كل ما يمكن أن يفعله الثلاثة المعتادون.
من الناحية العملية ، يعني هذا أنه يمكن بناء كل دائرة في الكمبيوتر باستخدام بوابة NAND فقط. في الممارسة العملية ، يحب المهندسون الإلكترونيون استخدام مجموعة متنوعة من البوابات لأنها أبسط.
NAND ليس المشغل العالمي الوحيد.
قد تعتقد أن NOR ، بمعنى آخر
NOT(P OR Q)
عالميًا أيضًا ولكن ماذا عن XOR؟ ليس هناك تلميح من بوابة NOT هنا – هل هناك؟
ومع ذلك ، ماذا عن P XOR صحيح؟
P True P XOR P
F T T
T T F
نعم ، P XOR True = NOT P ومن هذا يمكنك بناء عامل AND و. XOR هو أيضا عامل عالمي لمنطق بوليان.
إنه شيء يدعو للتفكير في أنه يمكن بناء المنطق بأكمله من عملية واحدة فقط.
[14] (Introduction to Boolean Logic ، بلا تاريخ)
اقترح للقراءة
إذا كنت بحاجة إلى مقدمة بسيطة لجانب الأجهزة من المنطق ، فإن Bebop إلى Boolean Boogie: دليل غير تقليدي للإلكترونيات من قِبل Clive Maxfield هي قراءة سهلة. إذا كنت تحب “For Dummies” ، فإن Logic For Dummies من Mark Zegarelli تستحق نظرة ولكن لاحظت أنها تتجاوز المنطق اللازم للحوسبة والمنطق الفلسفي. للحصول على مقدمة أكثر جدية ، لكنها جافة وحسابية ، جرب: جبر بوليان وتطبيقاته بقلم J. Eldon Whitesitt.Great أخيرًا ، على الرغم من نفاد طبعته ، إلا أن الأفكار في نظرية المعلومات واللغة وعلم التحكم الآلي من قبل Jagjit Singh قراءة جوهرية للعديد من المواضيع في حقيبة باباج .
ويمكنك معرفة المزيد حول هذه الكتب في اللوحات الجانبية لهذه المقالة.

الخاتمة
أعطني رأيك في التقرير
وفي الختام وقبل أن نضع جهدنا المتواضع هذا بين أيدي القراء نستخلص أنَّ جبر بول، هو مجرد طريقةٌ أخرى للنظر إلى المعطيات والبيانات، وقد ساهم عبر أسسه ومبادئه وعملياته بتقديم الأساس الصلب واللازم للثورة الرقمية، التي تم عبرها ابتكار الحاسوب الرقمي في خمسينيات القرن الماضي، وذلك بعد أن قام العالم الشهير كلود شانون بوضع أسس نظرية المعلومات، ومن ثم ومع انطلاق ثورة أنصاف النواقل على يد وليام شوكلي الذي ابتكر الترانزيستور، أصبح بالإمكان أن يصبح “الحاسوب” حقيقةً واقعية وهو ما أصبح عليه الآن. المعلومات في الحاسوب ترمز اعتماداً على القيمتين المنطقيتين “0” و “1”، وتقوم عبارات الجبر البولياني والتوابع المنطقية بتوصيف عمل البوابات المنطقية الإلكترونية التي تشكل الدارات الحاسوبية، وبالتالي، فإنه لم يكن من الممكن الحصول على ثورتنا الرقمية اليوم، لولا الجبر البولياني وعملياته ومعادلاته.
نأمل أن نكون قد قدمنا جميع المعلومات الأساسية لهذا الموضوع البسيط، ونتمنى أن نكون قد وفقنا في تقديم هذا البحث المفيد وتحقيق الهدف الذي أسعى من خلاله إيصال المعلومات المهمة إلى جميع القراء.

سأكون سعيداً للتواصل معي لأية آراء او تعليقات على بريدي الإلكتروني
الملاحق
الرياضيات المستخدمة في علوم الحاسوب
1) الرياضيات المتقطعة:
يُعرف هذا الفرع بدراسته للبُنى الرياضية التي تكون متقطعةً أساساً كمجموعةِ الأعداد الصحيحة، ذُكر هذا المصطلح أولاً في عام 1980 ليجمع العناوين الرياضية المهمّة لطلاب علوم الحاسوب، ثم تطورت لتشمل طرق التفكير بحلِّ المشاكل الواقعيّة باستخدام النماذج الرياضية والحاسوبية. تتعامل الرياضيات المتقطعة غالباً مع المنطق والاستنتاجات أكثرَ منها مع الأرقام، وعادةً ما يبدأ طلابها بتعلّم العبارات المنطقيّة والبراهين الرياضيّة والقدرة على إثبات الفرضيات لكميّاتٍ غيرِ محدودةٍ من البيانات باستخدام خطوتين محدودتين. لذلك وعندما تقوم بتصميم البرامج التي تعمل على ملايين الأجهزة، ستجعلك هذه الأداة على ثقةٍ بأنَّ الخوارزميات المُستخدَمة ستعملُ بشكلٍ صحيح، بغضِّ النظر عن البيئة التي ستعمل بها. وبالطبع فإنَّ الرياضيات المتقطّعة لديها مواضيعُها العددية، فدراسة خوارزميات الـمتتاليات الجمعية ستساعدك في تحسين الخوارزميات المُطبّقة ضمن الـ big-O، إضافةً لدراسة المصفوفات والأشعة التي تُعطي مَدخلاً جيداً لفهم المنطق المُستخدم عند التعامل مع المجموعات الضخمة للبيانات. استَخدمت العديدُ من شركاتِ وادي السيليكون كـ غوغل وياهو نظريةَ البيانِ عند بدئِها بتطوير خوارزميات الإنترنت، وتُعتبر نظريّة البيان أحدَ الفروع الهامّة في الرياضيات المتقطعة، حيثُ تُستخدم لنمذجةِ العلاقة بين العناصر، كما تُستخدم لنمذجةِ أيّةِ خوارزميةٍ بشكلٍ عمليّ، فبعدَ النّمذجة على أساسٍ بيانيٍّ يُمكن حلُّها باستخدامِ عملياتٍ خاصّة. وكما ذكرنا سابقاً فإنَّ مصطلح الرياضيات المتقطّعة متّسعٌ ويُعرَف على أنّه الوسيلة التي تجمع أهمَّ مواضيعِ الرياضيّات المهمّة لعلوم الحاسوب، فكلما ازداد إلمام الطالب بهذه المواضيع كلما ازدادت قدرته على مواجهة تحديات هندسة البرمجيات.
2) الاحتمالات:
الاحتمالات هي دراسة كل الاحتمالات التي من الممكن حُدوثها ضمن حدثٍ معيّن، يُصنَّف هذا المجال من الرياضيات عادةً ضمنَ الرياضيات المتقطّعة، لكنّه يمتلك العديد من التطبيقات خارجَ نطاق علوم الحاسوب ،وللاحتمالات دورٌ هامٌّ في تحديد كيف يمكن للبرنامج أن يعمل. باعتبار لدينا خوارزميةٌ لترتيب الأعداد تنازلياً، توقُّعُ سرعةِ أداءِ عمليةِ الترتيب يعتمدُ على عدّة عوامل، والطريقةُ التي يتمُّ تصميمُ الخوارزميّةِ باستخدامِها قد تؤثّر على سرعة تنفيذها، مع الأخذِ بعين الاعتبار حالاتِ البيانات المتوقَّعة سواءً الأفضل منها أو الأسوء أو المتوسط، وستساعدك الاحتمالاتُ لتحدّد فيما إذا كانت المعطياتُ موضوعةً بأسوأ ترتيبٍ أو أفضلِ ترتيبٍ وستساعدك للوصول للحل الأفضل. مهندسُ البرمجيات الجيّد يطرحُ جميعَ الأسئلة المتعلّقة بتصميمه، والاحتمالاتُ هي أفضل وسيلةٍ لطرحِ مثل هذه الأسئلة.
3) الجبر الثنائي والجبر البولياني:
نعلم أنَّ الحاسوب في مستوياتِه الأدنى هو عبارةٌ عن عددٍ كبير من الأصفار والواحدات المنطقية، فكيف تُتوّج هذه الأرقام على شكل مواقع ويب ومعالجات نصوص وألعاب؟ حسناً، يقوم الحاسوب بجمع ومقارنة هذه الأرقام باستخدام جبر بول، وهو أداةٌ تسمح أيضاً للمهندسين ببناء منطقٍ فعّالٍ عند بناء خوارزميّاتهم. هناك قيمةٌ كبيرةٌ لدراسة التّفاعل بين الأرقام الثّنائية في الحاسوب، فعلى سبيل المثال، ماذا سيفعلُ الحاسوب إذا كانت نتيجةُ الإضافة أو الضرب لا تتّسع في المكان المخصص لها (والذي غالباً ما يكون 32 بت)؟ إضافةً إلى أنّ العدد 0.1 هو عددٌ دوريٌّ لا نهائيٌّ في الأساس الثنائي (كما هو الحال للعدد ⅓ في الأساس العشري)، فكيف لذلك أن يؤثّر عليك كمبرمج؟ إنّ فهمَ واستيعابَ الدقةِ المحدودةِ للحاسوب ستمكّنك من نمذجة تطبيقات العالم الحقيقي والّتي تملكُ درجاتٍ غيرَ متناهيةٍ في الدّقة، مما سيعطيكَ دفعةً أعلى بين محترفي برمجة الحاسوب.
4) العودية:
عادةً ما يرى الحاسوبُ ما يقاربُ 20% من الشيفرة البرمجية تعملُ معظم الوقت، أي ما يقارب 80% من وقت تنفيذ البرنامج، ويُدعى هذا بقانونِ 80-20 والذي يؤدّي إلى استدعاء توابعَ برمجيةٍ معيّنةٍ أكثرَ من غيرها. ومن الممكن أن يقوم مهندسُ البرمجيات باستخدامِ أحدِ التّوابع للحصول على نتيجةٍ معينة، ثمّ يقومُ بتمرير هذه النتيجة إلى نفس التابع مرةً أُخرى، أو أن يقوم التابع باستدعاء نفسه. يُطلق على هذا المفهوم اسم “العَودية”، ويسمى المصطلح الرياضي الممثلُ لها بالتكرار. المثالُ الأكثرُ شيوعاً لمفهوم التكرار هو مسألة أبراج هانوي، حيث يتوجّب على المستخدم نقلُ الأقراص الموجودة على أحد الأعمدة إلى عمودٍ آخر مستخدماً عموداً وسيطاً، يمكن إيجادُ عددِ الخطوات اللازمة لحلّ هذه المسألة بتطبيقِ بعضِ القواعد الجبرية على عددٍ أقلَّ من العدد الكلّي للأقراص بمقدار 1 (n-1). نستطيع حلَّ هذه المسألة حاسوبياً باستخدام العودية، وذلك باستدعاء ذات التابع مراراً وتكراراً حتى نصل لما يسمى بالحالة القاعدية (base case) والتي تُعتبر أبسطَ أجزاء المُشكلة وذاتَ حلٍّ معلوم، ومن ثم نقوم بالبناء وفق هذا الحل. عادةً ما تُعتبر العَودية واحدةً من أولى المسائل “الصعبة” لطلاب علوم الحاسوب، ولكن عند فهم الرياضيات الكامنة وراء العودية ستساعدك على فهم وحلِّ العديد من المشاكل، وأيضاً ستلعب دوراً هاماً في فهم عملية تدفق البرامج. وننوه إلى أنّ الطريقة المثلى لدراسة العَودية هي عبر حلِّ العديد والعديد من المسائل الواقعية بطريقةٍ حاسوبية. تُعتبر المواضيع السابقة هامّةً وحساسةً لجميع مختصّي علوم الحاسوب، ونرى استخداماتها في معظم التطبيقات الحاسوبية اليومية، هل تعرف أيضاً فرعاً رياضياً مستخدماً بكثرة ضمن هذا المجال، ما هو؟ وما هي تطبيقاته؟
علاقة الحاسب الالي بجميع العلوم الاخرى
علاقة الحاسوب بعلم النفـــــس:
لماذا اهتمت السيكولوجيا بالحاسوب ؟
لقد عرفت السيكولوجيا المعرفية تقدما ملحوظا بفعل تطور الحواسيب التي شبهت بالدماغ و الذهن الإنساني فيما يخص عمليات التفكير الإنساني من جهة، والعمليات التي يقوم بإنجازها الحاسوب ordinateur من جهة أخرى .هذه التشبيهات عدت على أساسها فرضيات عمل قابلة للاستثمار من قبل الباحثين السيكولوجيين ،خصوصا ما توفره من إمكانيات التمييز بين جانب مادي (hardware ). و جانب برمجي (software) الذي بإمكانه الاشتغال دون التدخل المباشر للجانب المادي ، و هذا ما سمح باستخلاص تشبيهات موحية حول العلاقة بين الدماغ (cerveau)و الذهن( esprit ) لدى الإنسان و عقد مقارنات معا الحاسوب ( الجانب المادي الإلكتروني و الجانب البرمجي logiciels- – .
تكمن أهمية الحاسوب في كونه جهازا يستقبل المعلومات و المعطيات من العالم الخارجي و يقوم بترميزها و معالجتها ثم يخزنها في عناوين خاصة في الذاكرة و بعد ذلك يستعملها فهو جهاز يتوفر على مدخلات (input) و مخرجات (output) .أي شبيها بالذهن الإنساني الذي يستقبل المعلومات من المحيط و يقوم بمعالجتها و تخزينها للاستعمال لاحقا.
لهذا ارتكز علماء النفس المعرفيين على محاولة استعمال إمكانيات الحاسوب لدراسة المعالجة المعرفية كما تحدث في الذهن بسبب صعوبة مراقبة الوظائف الذهنية المعقدة ( كالذاكرة، التفكير،اللغة…..) التي تجري في الدماغ (العلبة السوداء) .بحث يكتفي الباحثين بمقارنة ” المدخلات ” و ” المخرجات ” و استنباط العمليات الواقعة بينهما. لقد
لقد ولد النجاح التكنولوجي لأجهزة معالجة المعلومات اقتناعا لدى العديد من الباحثين بأن الجهاز المعرفي الإنساني يخضع لقواعد الحاسوب نفسها . الدماغ البشري ليس إلا جهازا ماديا من بين أجهزة أخرى يتدفق إلى جهازه المعرفي (الذهن) سيل من المعلومات يقم بتمثلها و معالجتها.و بفضل تطر الإعلاميات انتشر الاتجاه “المعرفي الحاسوبي” المتمركز حول “معالجة المعلمات”، مقيما تشابها بين الإنسان الحاسوب ،فكليهما يستقبل المعلومات من الخارج يعالجها في سلسلة من المراحل ،ثم يقم بتخزينها في مستويات عدة. بذلك يعتبر الإنسان مجموعة من معالجات -processeurs – المعلومات .
و انطلاقا من هذه التشبيهات الموحية حول العلاقة بين الدماغ والذهن لدى الإنسان. تطور منهج النماذج (Modèles)الذي يقدم إسهامات هامة في تطوير دراسة الذاكرة المعجمية وتقييسها). وبذلك أصبحت نماذج التقييس تفرض نفسها على التيارات المعرفية بسبب طابعها العلمي والتكنولوجي الذي اكتسبته من علاقاتها بالعلوم العصبية والذكاء الاصطناعي )، كما أصبح السيكولوجيون المعرفيون يلجؤون إلى تقنيات علوم الحاسوب للتعبير عن نماذج عمليات التفكير الإنساني.
و كذلك لدراسة أنواع الذاكرات لدى الإنسان.
الحاسب الالي وعلم الفيزياء:
قد يسأل البعض منا ما علاقة الحاسب الالي بعلم الفيزياء ؟ انها علاقة كبيرة فمواد الحاسب الالي وفكرة عملها اساسا مأخوذن من هذا العلم الكبير ففي علم الفيزياء يوجد فرع اسمه اشباه الموصلات فكما نعلم ان المواد ثلاث انواع موصلة وعازلة وشبه موصلة وهي التي تكون مقاومتها موصلة اي ليست موصلة ولا عازلة والمواد شبه الموصلة تستخدم في صناعة مكونات الحاسب الالي فنري الميكروبروسيسور وهو عقل الحاسب الالي مصنوع من مواد شبه موصلة مثل مادة السيلكون وصناعة الترانزستورات الموجودة في الميكروبروسيسور ،هذا العلم كبير جدا ولمن يريد ان يعرف اكثر يضغط علي اللنك القادم ……
الحاسب الالي وعلم الرياضيات:
طبعا كلمة حاسب مأخوذة من الحسابات او الارقام وعلم الرياضيات فنلاحظ في الحاسب الالي يوجد المنطق الرياضي والاستنتاج والمصفوفات والمتسلسلات والمحددات وهذا هو علم الجبر فرع من علم الرياضيات ، ونلاحظ ايضا تطبيقات الاحتمالات في البرامج وايضا مبادئ التحليل العددي وحلول التفاضل والتكامل والمعادلات التفاضلية كل هذا نستخدمه في البرامج في الحاسب الالي ونلاحظ ايضا نظرية الخوارزميات وكيفية تحليل المشكلة البرمجيه وكثير وكثير ….فالبرمجة كما ستلاحظون بها اشياء كثيرة رياضيه ولكن سهلة جدا ليس كما تتصورون …
الطـــــــــب :
دخل الحاسب مجال الطب فالاجهزة التي نشاهدها سواء اجهزة العمليات او الاجهزة التليفزيونينة المستخدمة في الاشعة وجميع الاجهزة الطبية مبنيه علي الحاسبات وايضا كشف الDNA هناك مشروع كامل يحلل هذا Human Genome Projectوكثير وكثير ……ز
2- الهــــــــــــندسة :
فهناك برامج كثيرة يستعملها المهندسون مثل برنامج Autocadويستخدم في التخطيط والرسم الهندسي…..
3- الاتصــــــــالات :
الحاسب الالي ايضا يستخدم في الاتصالات واجهزة الشبكات ولمن يريد يعرف اكثر يبحث عن هذا الموضوع..
4- الفــــــــــلك :
اجهزة التلسكوبات والاقمار الصناعيه والكشف عن الكواكب كلها دخل فيها الحاسب الالي وتطور هذا العلم بالحـــــــاسب الالي
5- الانترنــــت :
الشبكة العنكبوتية اصبحت ملايين الاجهزة يمكنها الاتصال معا في شبكة واحدة وتحت بروتوكولات معينة واصبح بامكان اي شخص ان يتعرف علي كل العالم وهو موجود في البيت فاصبح العالم عبارة عن قرية صغيرة …….
6- مجـــالات اخـــــــري:
كما نعلم جهاز ATM وهو الجهاز الذي نراه في البنوك لنضع فيه Master Cardالذي نستعملها لسحب النقود هذه الالة ما هي الا جهاز به برنامج مكتوب بلغة معينة وينفذ اوامر معينة .
· العدد القادم نكشف ألارتباط الوثيق بين الحاسوب وإدارة الأعمال والأقتصاد
المنطق البوليني
منطق بوليان من السهل جدا أن يشرح ويفهم.
- عليك أن تبدأ بفكرة أن بعض العبارات P إما صحيحة أو خاطئة ، فلا يمكن أن يكون بينها شيء (يطلق عليه قانون الوسط المستبعد).
- بعد ذلك ، يمكنك تكوين عبارات أخرى ، صحيحة أو خاطئة ، من خلال الجمع بين هذه العبارات الأولية معًا باستخدام العوامل الأساسية And و Or و Not.
بالضبط ما هو المشغل “الأساسي” الذي يشكل سؤالًا مثيرًا للاهتمام بحد ذاته – شيء سنعود إليه لاحقًا عندما نسأل كم عدد العوامل المنطقية التي نحتاجها بالفعل؟
تتناسب الطريقة التي يعمل بها كل هذا إلى حد ما مع الطريقة التي استخدمنا بها هذه المصطلحات باللغة الإنجليزية.
على سبيل المثال ، إذا كانت P صحيحة ، فإن Not (P) خاطئة. لذا ، إذا كانت “day is Monday” صحيحة ، فإن “Not (اليوم هو الاثنين)” خاطئة.
غالبًا ما نترجم التعبير المنطقي إلى اللغة الإنجليزية كـ “اليوم ليس الاثنين” ، وهذا يجعل من السهل معرفة أنه من الخطأ إذا كان اليوم هو يوم الاثنين بالفعل.
هل نتابع؟
حسنا هذه هي المشكلة مع هذا النوع من النقاش. يصبح سريعًا معقدًا ويصعب متابعته وهذا جزء من قوة المنطق البولياني. يمكنك كتابة الحجج بوضوح في شكل رمزي.
الجداول الحقيقة
عادة ما يتم تدوين قواعد دمج التعبيرات كجداول تسرد جميع النتائج المحتملة. تسمى هذه الجداول بجداول الحقيقة وثلاث عوامل أساسية:
P Q P AND Q
F F F
F T F
T F F
T T T
P Q P OR Q
F F F
F T T
T F T
T T T
P NOT P
F T
T F
لاحظ أنه بينما يكون Boolean And هو نفس استخدام اللغة الإنجليزية للمصطلح ، فإن Boolean Or مختلف قليلاً.
عندما يُطلب منك أن تحب “قهوة أو شاي” ، لا يُتوقع منك أن تقول نعم لكليهما!
في الحالة المنطقية ، فإن كلمة “أو” تتضمن بكل تأكيد كليهما. عندما يكون P صحيحًا و Q صحيحاً ، يكون التعبير المشترك (P أو Q) صحيحًا أيضًا.
هناك عامل منطقي يتوافق مع استخدام اللغة الإنجليزية للمصطلح “أو” ويطلق عليه “الحصري أو” مكتوب كـ EOR أو XOR. جدول الحقيقة هو:
P Q P XOR Q
F F F
F T T
T F T
T T F
وهذا من شأنه أن يمنعك من تناول الشاي والقهوة في نفس الوقت (لاحظ أن السطر الأخير هو True XOR True = False).
جداول الحقيقة العملية
كل هذا يبدو سهلاً للغاية ولكن ما قيمة ذلك؟
من المؤكد أنه ليس نموذجًا للتفكير اليومي ماعدا مستوى “القهوة أو الشاي” الأقل أهمية او بعيارة أخرى الأكثر تفاهة ?.
نحن نستخدم منطق بوليان في تفكيرنا ، والسياسيون ربما لا يفعلون ذلك ولكن هذه قصة أخرى ، ولكن فقط على المستوى الأقل أهمية ?.
ومع ذلك ، إذا بدأت في تصميم الآلات التي يجب أن تستجيب للعالم الخارجي بطريقة معقدة بشكل معقول ، فسوف تكتشف بسرعة أن المنطق البولياني هو مساعدة عظيمة.
على سبيل المثال ، لنفترض أنك تريد إنشاء نظام أمان يعمل فقط في الليل ويستجيب إلى باب يتم فتحه. إذا كان لديك جهاز استشعار للضوء ، فيمكنك التعامل مع ذلك كإعطاء إشارة تشير إلى صحة العبارة:
P = إنه النهار.
من الواضح أن (P) غير صحيح عندما يكون الليل ، ولدينا أول استخدام عملي لمنطق بوليان!
ما نريده حقًا هو شيء يعمل على حقيقة البيان:
R = السطو قيد التقدم
من ف و
Q = نافذة مفتوحة
وهناك القليل من التفكير الخام قريبا يعطي الحل
R = ليس (P) و Q
هذه هي حقيقة “السطو قيد التقدم” التي قدمها جدول الحقيقة التالي:
P Q NOT(P) NOT(P)AND Q
F F T F
F T T T
T F F F
T T F F
من هذا ، يجب أن تكون قادرًا على رؤية أن المنبه ينفجر فقط عندما يكون الوقت ليليًا ويفتح نافذة.
المنطق البوليني وأنظمة الترميز
انظمة الترميز هى برمجيات عالمية تساعد الكمبيوتر على عرض اللغات العالمية
ومن اشهرها اليونيكود هو ترميز الاتحاد الاوربى وحالياً يعتبر عالمى
وكل ترميز يقوم بتعريف عدة لغات يوجد تراميز من اليونيكود حسب البلد لا تعرض اللغه العربيه
ومنها لا يعرض الصينية واخرى كثيرة لذالك انظمة الترميز مهمه لعرض اللغات.
الترميز Coding
هو قاعدة لتحويل معلومة (على سبيل المثال، حرف، كلمة، عبارة أو إشارة) إلى شكل أو تمثيل آخر – عادة مختصر أو سري – (علامة واحدة مقابل علامة أخرى)، وليس بالضرورة من نفس النوع أو الطول . في مجال الاتصالات communications ومعالجة المعلومات Information processing، الترميز encoding، هو العملية التي من خلالها يتم تحويل المعلومات من المصدر Source إلى رموز symbols ليتم إيصالها ألى الهدف Target. فك الترميز Decoding هو عملية عكسية، وهو تحويل هذه الرموز رجوعا إلى معلومات مفهومة من قبل المتلقي. أحد أسباب اللجوء إلى الترميز هو لتمكين الاتصال في الحالات التي يستحيل، أو يصعب، استخدام اللغة العادية الصريحة، منطوقة كانت أم مكتوبة. على سبيل المثال، أعلام الإشارة، Semaphore، حيث ترتيب الأعلام التي بحوزة المشير Signaller، أو مجهز بها برج الإشارة، ترمّز أجزاء من رسالة، عادة حروف وأرقام. يمكن لشخص آخر يقف على مسافة كبيرة بعيدا تفسير الأعلام واستخراج الكلمات المرسلة.
النظرية
في نظرية المعلومات Information theory وعلوم الحاسوب Computer science، عادة ما يعد الترميز خوارزمية تعطي رمزا فريدا من أبجدية ما كمصدر ، بوساطة سلسلة String مرمزة، والتي قد تكون في أبجدية أخرى مستهدفة. يتم الحصول على توسيع الترميز، لتمثيل متوالية من الرموز على الأبجدية المصدر بواسطة وصل concatenate السلاسل المرمزة. قبل إعطاء تعريف دقيق رياضيا، نعطي مثالا وجيزة.

References
Boolean Logic and Digital Circuits. (n.d.). Retrieved from The Electropaedia: https://www.mpoweruk.com/digital_logic.htm#xor
Boolean logic in Programming Languages. (n.d.). Retrieved from Math Wiki: https://math.wikia.org/wiki/Boolean_logic_in_Programming_Languages
By Chetvorno (Own work) [CC0], v. W. (n.d.). Computer Engineering: How do we explain to someone how Boolean logic is applied in (hardware) circuits, using logic gates, to solve a real world problem? (B. C. Andrew Silverman, Editor) Retrieved from Quora: https://www.quora.com/Computer-Engineering-How-do-we-explain-to-someone-how-Boolean-logic-is-applied-in-hardware-circuits-using-logic-gates-to-solve-a-real-world-problem/answer/Andrew-Silverman-10
Introduction to Boolean Logic . (n.d.). Retrieved from I Programmer: https://www.i-programmer.info/babbages-bag/235-logic-logic-everything-is-logic.html?start=2
Math, Math for Computer Science: Discrete. (n.d.). Retrieved from Masters Program in Computer Science: https://masters.cs.uchicago.edu/page/math-needed-computer-science
د. زهير دحروج. (بلا تاريخ). نمط المتحولات المنطقية Boolean. دمشق.
